霍尔编码器简要笔记

轮趣 MG370P34_12V 电机采用的是磁式霍尔增量编码器，主要由多对极磁环和霍尔元件组成。

MG370 电机所带的霍尔 AB 相编码器属于增量式编码器（区别于 AS5600 这类磁性绝对角度传感器），其输出的 A、B 两路信号具有固定的相位先后关系，可用于判断电机转动方向，并统计转速及转动角度增量。由于该编码方式不提供绝对位置信息，上电后需从初始状态开始累计。其结构简单、响应实时性好，特别适合用于直流电机的速度闭环控制和相对位移测量，是 PID 调速系统中常用的反馈方案。

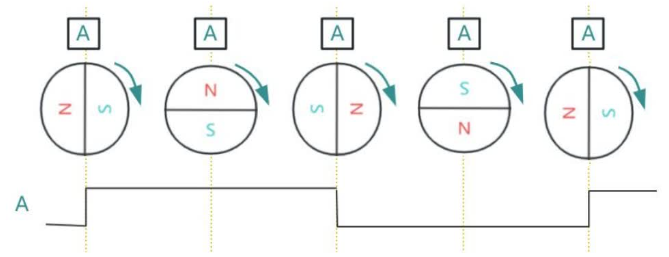
磁环安装在电机轴上，与电机同轴旋转。磁环圆周上等分排列 N 极与 S 极，形成若干对磁极；霍尔元件固定不动，用于检测磁环经过时的磁极变化。当霍尔元件检测到 N 极或 S 极时，会分别输出高、低电平信号。

当电机持续转动时，磁环随轴旋转，N/S 极不断交替经过霍尔元件，因此编码器输出连续的方波信号。
在最简单的情况下，如果磁环只有 1 对极，且只有 1 个霍尔元件，那么磁环旋转一圈，霍尔元件就会输出 一个周期的方波。磁环极对数越多，每转一圈输出的脉冲数就越多，角度分辨率也越高。

实际的磁环上不仅仅是一个对极，当磁环有N个对极时电机轴转动一圈可以输出N个周期的方波，对实际磁环进行测量可以看出，一个多极性磁环共有13对极，也就是电机的编码器精度为13。

from machine import Pin
import time

# 你的A相引脚（改成实际的）
enc_a = Pin(8, Pin.IN, Pin.PULL_UP)

count = 0

def callback(pin):
    global count
    count += 1  # 只计数A上升沿（最简单方式）

enc_a.irq(handler=callback, trigger=Pin.IRQ_RISING)

print("准备好了！慢慢正向转电机轴正好10圈或20圈，看count变化")

# 运行后转动，完成后Ctrl+C中断或等30秒
time.sleep(30)  # 给你时间转

print("累计脉冲（A上升沿）:", count)
print("转圈数（手动数）: 比如10圈")
print("PPR = 累计脉冲 / 转圈数")

# result
# >>> %Run -c $EDITOR_CONTENT
# 准备好了！慢慢正向转电机轴正好10圈或20圈，看count变化
# 累计脉冲（A上升沿）: 26
# 转圈数（手动数）: 比如10圈
# PPR = 累计脉冲 / 转圈数
# 结论：2圈26个脉冲数，1圈13

MG370P34_12V 使用的是 AB 相双通道输出。A 相与 B 相之间存在固定的相位差（接近正交），这种设计的核心目的是判断电机转动方向：

1）A 相先变化，B 相后变化 → 正转

2）B 相先变化，A 相后变化 → 反转

对于程序来说通过，A相来一个上升沿或者是下降沿的时候，如果B相是高电平就认为是正转，低电平就认为是反转。

from machine import Pin

# 定义引脚
ENC_A = Pin(8, Pin.IN, Pin.PULL_UP)
ENC_B = Pin(9, Pin.IN, Pin.PULL_UP)

# 定义全局变量
velocity = 0

# 编码器中断回调函数
def read_encoder(pin):
    global velocity
    # 获取当前A相和B相的电平
    a_state = ENC_A.value()
    b_state = ENC_B.value()

    # A相发生跳变时，判断B相的电平
    if a_state == 1:  # A相上升沿
        if b_state == 0:
            velocity += 1  # B相低电平 → 正转（1 0）
        else:
            velocity -= 1  # B相高电平 → 反转（1 1）
    else:  # A相下降沿
        if b_state == 1:
            velocity += 1  # B相高电平 → 正转（0 1）
        else:
            velocity -= 1  # B相低电平 → 反转（0 0）

# 为A相引脚添加上升沿和下降沿中断
ENC_A.irq(trigger=Pin.IRQ_RISING | Pin.IRQ_FALLING, handler=read_encoder)

频率等于周期的倒数，因此通过波形频率可以反推出单个脉冲的周期长度；进一步可知在 1s 内会产生多少个脉冲。结合电机的减速比与编码器精度，即可按照前文公式计算电机转速。

以上图为例，若测得编码器输出波形频率约为 833 Hz，则表示：1 s 内约有 833 个周期方波 假设：

• 电机减速比为 30
• 编码器精度为 13（每转输出 13 个脉冲）

则电机输出轴转速为：$ 833 / (30 × 13) ≈ 2.14 $ r/s（圈/秒）
换算为 RPM：$ 2.14 × 60 ≈ 128 $ RPM
若电机轴上安装的轮子周长为 30 cm = 0.3 m，则线速度为：$ 2.14 × 0.3 ≈ 0.64 $ m/s

由此可见，通过测量编码器输出波形频率，并结合减速比与编码器精度参数，即可完成从脉冲信号到转速、再到线速度的完整换算。

单片机通过采集 AB 相的脉冲数量和相位顺序，可以实现：

• 脉冲计数 → 位置（增量）计算
• 脉冲频率 → 转速计算

该霍尔编码器结构简单、成本低、抗干扰能力强，广泛用于直流减速电机的速度与位置反馈场景。

from machine import Pin
import time

# 定义引脚
ENC_A = Pin(8, Pin.IN, Pin.PULL_UP)
ENC_B = Pin(9, Pin.IN, Pin.PULL_UP)

# 定义全局变量
step_count = 0       # 累计步数（替代原来的velocity，命名更直观）
last_time = time.ticks_ms()  # 记录上一次计算速度的时间
rpm = 0              # 转速（转/分钟）
encoder_lines = 100  # 编码器线数（根据你的实际编码器修改！）

# 编码器中断回调函数（核心逻辑不变）
def read_encoder(pin):
    global step_count
    a_state = ENC_A.value()
    b_state = ENC_B.value()

    # 根据真值表逻辑判断电机正反转
    if a_state != b_state:
        velocity += 1  # 正转
    else:
        velocity -= 1  # 反转

# 清零计数和转速的函数
def reset_encoder():
    global step_count, rpm
    step_count = 0
    rpm = 0
    print("编码器计数已清零！")

# 计算转速的函数
def calculate_rpm():
    global step_count, last_time, rpm
    current_time = time.ticks_ms()
    time_diff = time.ticks_diff(current_time, last_time) / 1000  # 时间差（秒）

    if time_diff >= 1:  # 每1秒计算一次转速
        # 计算逻辑：
        # 1. 双沿计数 → 每转步数 = 编码器线数 × 2
        # 2. 每秒步数 ÷ 每转步数 = 每秒转数 → ×60 = 每分钟转数（RPM）
        steps_per_second = abs(step_count - 0) / time_diff  # 每秒步数
        rpm = (steps_per_second / (encoder_lines * 2)) * 60

        # 重置计时和临时计数
        last_time = current_time
        step_count = 0  # 清空累计步数，用于下一秒计算

# 为A相引脚添加上升沿和下降沿中断
ENC_A.irq(trigger=Pin.IRQ_RISING | Pin.IRQ_FALLING, handler=read_encoder)

# 主循环：实时显示转速+支持手动清零（示例）
if __name__ == "__main__":
    print("编码器测速程序已启动！")
    print("提示：step_count为累计步数，rpm为转速（转/分钟）")
    while True:
        calculate_rpm()  # 每秒计算一次转速
        # 打印实时数据
        print(f"累计步数：{step_count} | 当前转速：{rpm:.1f} RPM", end="\r")
        time.sleep(0.1)  # 刷新频率（可调整）

        # 【可选】按需求触发清零（比如检测某个引脚电平/按键）
        # 示例：如果Pin(10)接低电平，触发清零
        # if Pin(10).value() == 0:
        #     reset_encoder()
        #     time.sleep(0.2)  # 消抖